ECC 椭圆曲线 - X̂ Blog

椭圆曲线密码学（Elliptic Curve Cryptography, ECC）是一种基于椭圆曲线数学的非对称式密码学算法。

ECC 的主要优势是它相比 RSA 加密算法使用较小的密钥长度并提供相当等级的安全性。

如今，在现代计算机网络技术中，比如 TLS、PGP 和 SSH，都有用到椭圆曲线加密算法。更不要说去中心化系统，如比特币和其它加密电子货币了。

椭圆曲线

椭圆曲线是由这个方程描述的平面曲线：

$$ y^2 = x^3 + ax + b $$

其中 $a$, $b$ 都是实数。上述方程就是所谓的魏尔斯特拉斯一般形式。

为排除退化成奇异曲线的情况，还需要满足 $4a^3 + 27b^2 \ne 0$。

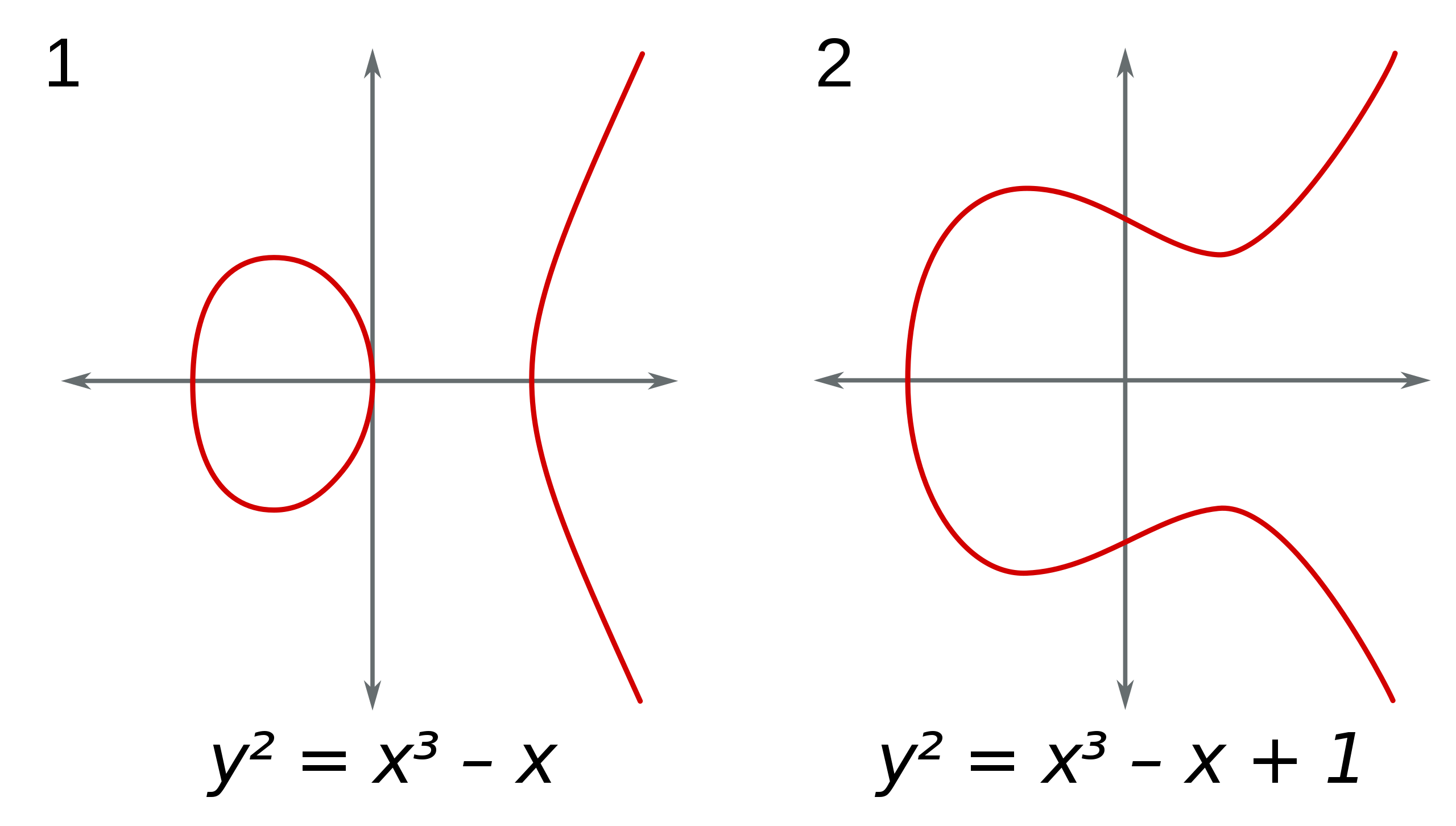
随着 $a$ 和 $b$ 取值的变化，椭圆曲线可能在平面上会呈现不同的性状。不论是直观还是证明，我们都可以发现椭圆曲线是关于 $x$ 轴对称的。

群

在数学中，群（Group）是由一个集合以及一个二元运算符所组成的代数结构，且符合以下四个性质：

封闭性：对于所有 $G$ 中的 $a$, $b$，运算 $a \cdot b$ 的结果也在 $G$ 中。
结合律：对于所有 $G$ 中的 $a$, $b$, $c$，等式 $(a \cdot b) \cdot c = a \cdot (b \cdot c)$ 成立。
单位元：存在 $G$ 中的一个元素 $e$，使得对于所有 $G$ 中的元素 $a$，总有等式 $e \cdot a = a \cdot e = a$ 成立。
逆元：对于每个 $G$ 中的 $a$，存在 $G$ 中的一个元素 $b$ 使得总有 $a \cdot b = b \cdot a = e$，$e$ 为单位元。

其中群 $(G,\cdot)$ 也常常简记为 $G$，符号「 · 」是具体的运算，比如整数加法。

如果我们添加第五条要求：

交换律：$a \cdot b = b \cdot a$

那么这个群就是阿贝尔群。

最常见的群之一是整数集 $Z$ 和整数的加法所构成的整数加法群。

基本概念

阶

群中元素个数称为群 $G$ 的阶，记为 $|G|$。

有限群

一个群被称为有限群，如果它有有限个元素。元素的数目叫做群 $G$ 的阶。

椭圆曲线的群律

我们可以在椭圆曲线上定义一个群。具体地说，

群的元素是椭圆曲线上的点，二元运算符为 $+$
单位元是无穷远点 $O$
点 $P$ 的逆是它关于 $x$ 轴的对称点

加法 $P + Q$ 通过如下法则定义：

过 $P$ 和 $Q$ 两点的直线与椭圆曲线相交于第三点 $R$，作 $R$ 关于 $x$ 轴对称的点 $R^\prime$，$R^\prime$ 是椭圆曲线上的点，则 $P + Q = R^\prime$。

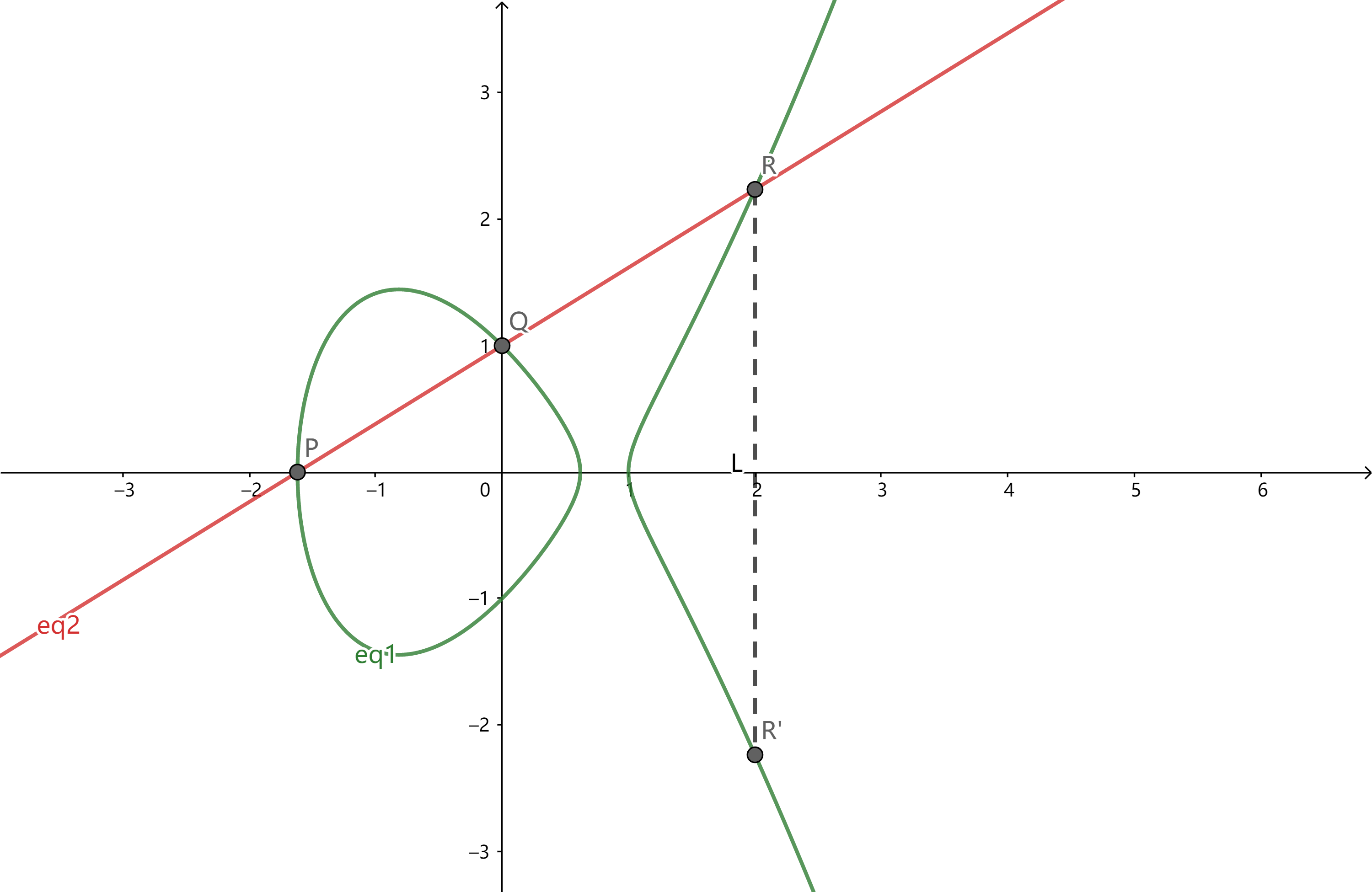
特殊情况说明：

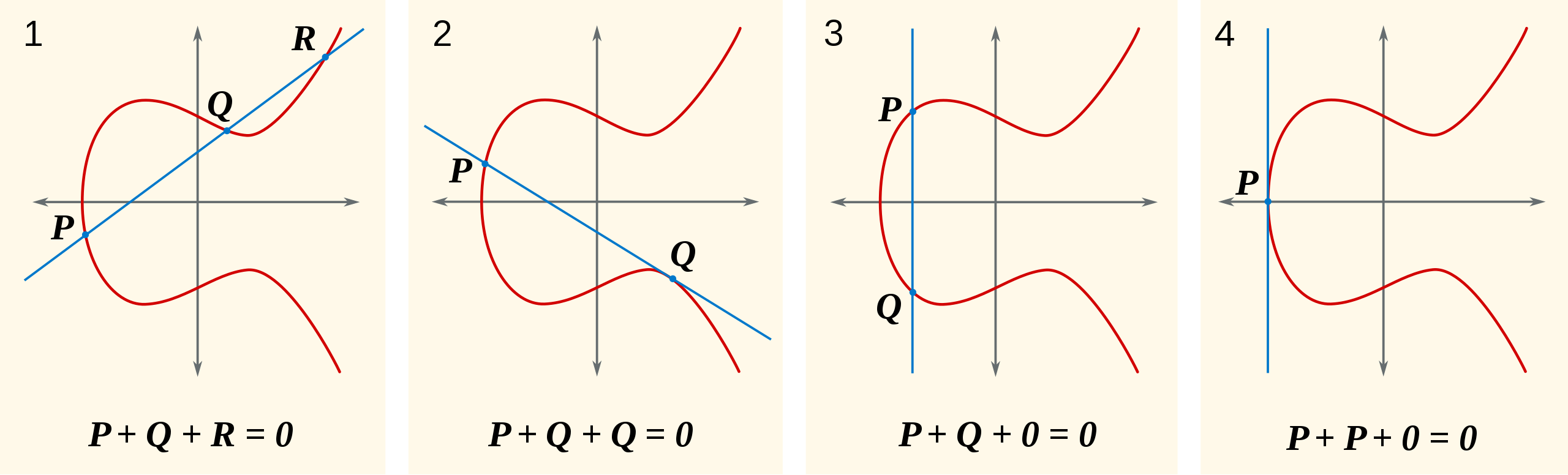
如果 $Q$ 是无穷远点，则 $P + O = O + P = P$，这使得无穷远点 $O$ 作为该群的单位元，满足单位元性质。
如果 $P$ 和 $Q$ 关于 $x$ 轴对称，则它们的第三个交点为无穷远点，$P + Q = Q + P = O$。而 $P$ 的逆为它关于 $x$ 轴的对称点 $Q$，椭圆曲线是关于 $x$ 轴对称的，满足逆元性质。为叙述方便，点 $P$ 的逆用 $-P$ 来表示。
如果 $P$ 与 $Q$ 相等，此时只有一个点，在这种情况下，有无数条直线过这个点。事情就变得有点复杂了。但我们可以先构想一个 $Q^\prime$ 点（$Q^\prime \ne P$）。如果 $Q^\prime$ 逐渐接近 $P$ 点，$PQ^\prime$ 会变成什么样？$PQ^\prime$ 直线会逐渐趋近曲线的切线。根据这个事实，我们能这样断言：过 $P$ 点作曲线的切线与曲线交于另一点 $R$，则 $P + P = -R$。
如果 $P \ne Q$，但找不到第三点 $R$ 怎么办？这种情况很像上一种。事实上，这种情况就是过 $P$，$Q$ 的直线是曲线的切线。它的和就是其中一个点关于 $x$ 轴的对称点。不妨设 $Q$ 点就是切点，在上一种情况，我们已经说明 $Q + Q = -P$，这个等式可以变成 $P + Q = -Q$。

显然，上面定义的群具有封闭性，而结合律 $(A + B) + C = A + (B + C)$ 这个结论的证明并不直观，下面一个例子可以更直观地理解。

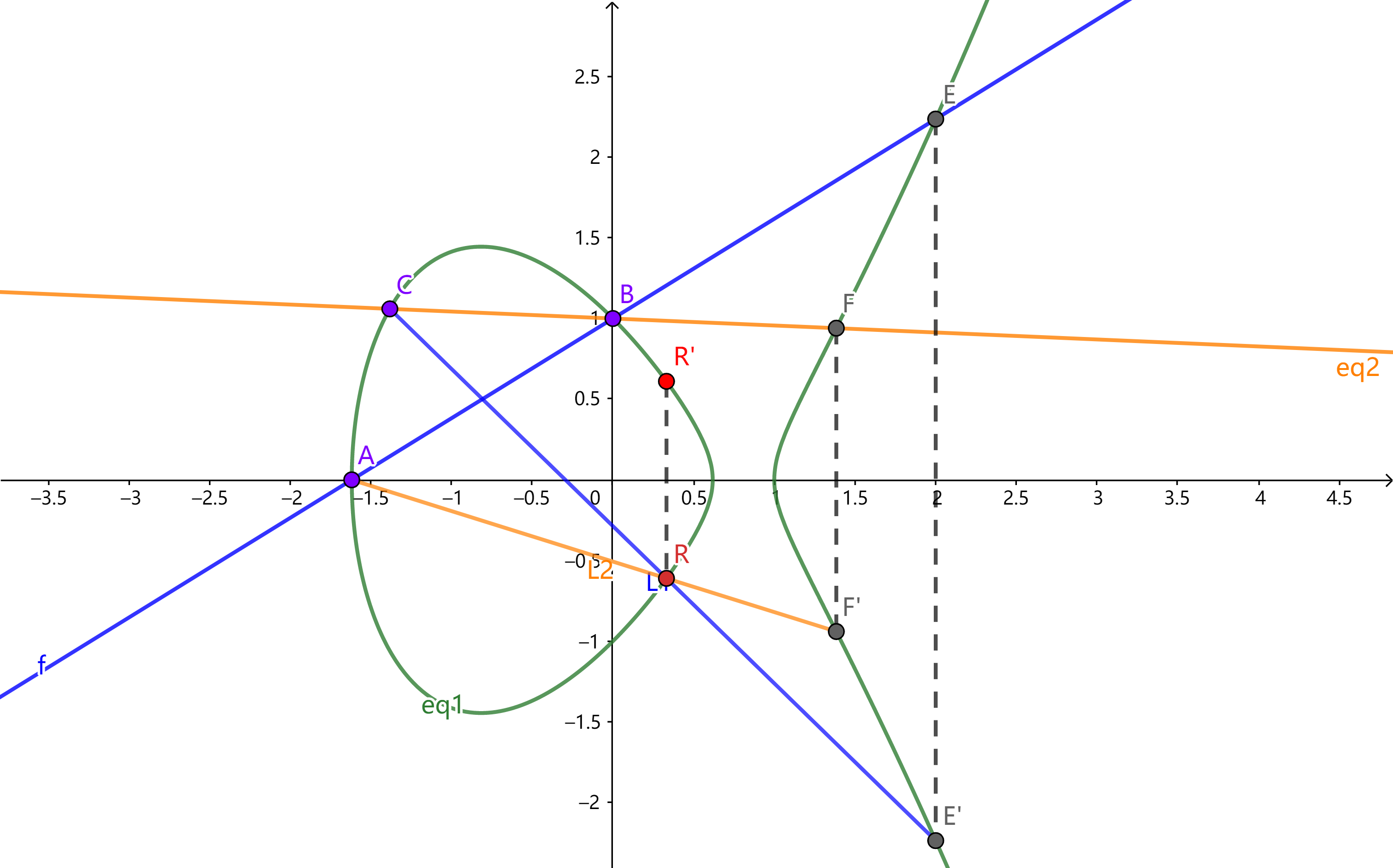
上图中绿色线为椭圆曲线，蓝色线为 $(A + B) + C$，橙色线为 $A + (B + C)$，可以看到最后 L1 和 L2 两条线都相交于同一个点 $R$，两式的结果都是 $R^\prime$ 点。

两点的加法为什么不直接用第三个交点作为最终的结果呢，显然这样的话是无法满足结合律的。经过上面的叙述，我们可以得出上面定义的群是阿贝尔群。

代数加法

给定曲线 $y^2 = x^3 + ax + b$，曲线上的两点 $P = (x_P, y_P)$，$Q = (x_Q, y_Q)$，其中 $x_P \ne x_Q$，则过 $P$，$Q$ 两点的直线方程为 $y = sx + d$，其中斜率 $s$ 为：

$$ s = \frac{y_P - y_Q}{x_P - x_Q} $$

我们需要求出直线与曲线的第三个交点 $R=(x_R, y_R)$，把 $y$ 代入曲线方程即可：

$$ {(sx+d)^2=x^3+ax+b} $$

展开式子，得

$$ {x^3-s^2x^2-2sdx+ax+b-d^2=0} $$

上述方程有三个根，也就是 $P$，$Q$，$R$ 三个点。

$$ (x - x_P)(x - x_Q)(x - x_R) = x^3 + x^2(-x_R-x_Q-x_P) + x(x_Qx_R+x_Rx_P+x_Px_Q) - x_Px_Qx_R = 0 $$

对比两个方程的系数可以求得

$$ x_R = s^2 - x_P - x_Q $$

又直线过 $P$ 点，可求出直线方程的截距 $d$：

$$ d = y_P - sx_P $$

最后根据直线方程，计算 $R$ 的 $y$ 坐标：

$$ y_R = y_P + s(x_R - x_P) $$

若 $x_P = x_Q$，可分为以下几种情况：

$y_P = -y_Q$
$y_P = y_Q = 0$
$y_P = y_Q \ne 0$

前两种情况根据前面的描述，和定义为 $O$。最后一种情况即 $P = Q$，需要求出曲线在 $P$ 点的切线。也就是需要对曲线进行求导。

$$ \frac{dy^2}{dx} = \frac{d}{dx} (x^3 + ax +b) =3x^2 + a $$

$$ 2y\frac{dy}{dx} = 3x^2 + a $$

$$ \frac{dy}{dx} = \frac{3x^2 + a}{2y} $$

此时过 $P$ 点的直线的斜率 $s$ 为

$$ s = \frac{3x_P^2+a}{2y_P} $$

$R$ 点的坐标为

$$ x_R = s^2 - 2x_P $$

$$ y_R = y_P + s(x_R - x_P) $$

数乘

除了加法，我们还可以定义另一种算符：数乘，即

$$ nP = \underbrace{P + P + \ldots + P}_{n} $$

直接相加的话，$nP$ 的计算需要 $n$ 次加法。如果 $n$ 有 $k$ 位二进制位，那算法复杂度就是 $O(2^k)$。

然而，我们能找到更快的算法：其中一个就是倍乘相加算法。

要计算 $nP$，我们把 $n$ 用二进制表示：

$$ n=2^0n_{0}+2^1n_{1}+2^{2}n_{2}+\cdots+2^{m}n_{m} $$

其中 $n_i \in \{0, 1\}$，$m = \lfloor \log_2n\rfloor$。所以 $nP$ 为

$$ nP = 2^0n_{0}P+2^1n_{1}P+2^{2}n_{2}P+\cdots+2^{m}n_{m}P $$

def bits(n):
    while n:
        yield n & 1
        n >>= 1

def double_and_add(n, x):
    result = None
    addend = x

    for bit in bits(n):
        if bit == 1:
            if result is None:
                result = addend
            else:
                result = add(result, addend)
        addend = add(addend, addend)

    return result

如果加和是复杂度为 $O(1)$ 的操作，那这个算法的复杂度就是 $O(\log n)$，这就相当优秀了。

有限域

域是个集合 $F$ 且带有加法和乘法两种运算。它是一个加法的阿贝尔群，0 为单位元；非零元素集合是一个乘法的阿贝尔群，1 为单位元，且满足乘法分配律。

有限域亦称伽罗瓦域（Galois Fields），是仅含有限个元素的域。其元素个数也跟域的阶数相同，一个有限域的阶总是一个素数的幂。

我们在前面讨论的都是实数域上的椭圆曲线，但密码学中并不直接使用，因为

实数域上的椭圆曲线是连续的，有无限个点，密码学要求有限个点。
实数域上的椭圆曲线运算是有误差的，不精确，密码学要求精确。

因此我们需要引入有限域上的椭圆曲线。

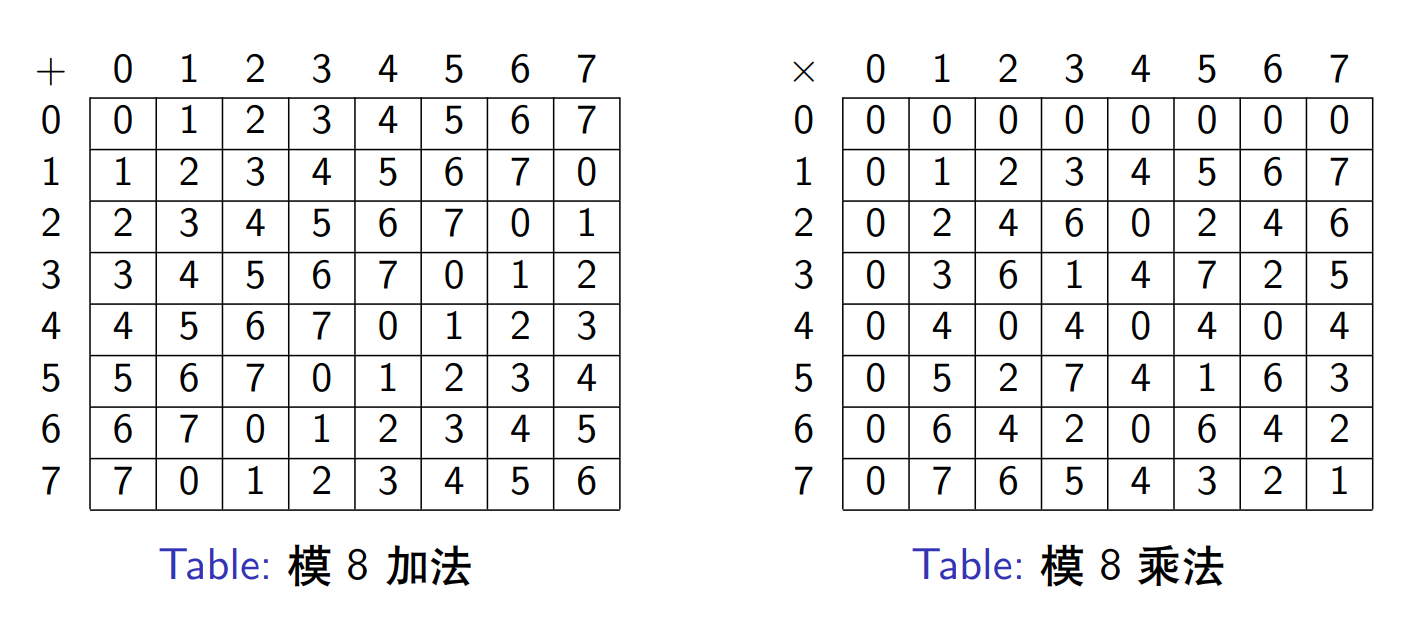
模算术

运算（mod n）将所有整数映射到集合 $\{0, 1, \ldots,(n − 1)\}$。因此，限制在这个集合的技术称为模算术。

性质：

$[(a \mod n) + (b \mod n)] \mod n = (a + b) \mod n$
$[(a \mod n) − (b \mod n)] \mod n = (a − b) \mod n$
$[(a \mod n) × (b \mod n)] \mod n = (a × b) \mod n$

运用以上性质，可以计算出模加法和模乘法两种运算的结果：

加法逆元

若存在 $z$，使得

$$ w+z=0 \mod n $$

则，$z$ 即为加法逆元 $−w$。

乘法逆元

若存在 $z$，使得

$$ w \times z=1 \mod n $$

则，$z$ 即为乘法逆元 $w^{-1}$。

$w$	0	1	2	3	4	5	6	7
$-w$	0	7	6	5	4	3	2	1
$w^{-1}$	-	1	-	3	-	5	-	7

从上表可以看出乘法逆元有不存在的情况。

性质

下面总结一下 $Z_n$ 中整数模运算的性质：

性质	表达式
交换律	$(w + x) \mod n = (x + w) \mod n$ $(w × x) \mod n = (x × w) \mod n$
结合律	$[(w + x) + y] \mod n = [w + (x + y)] \mod n$ $[(w × x) × y] \mod n = [w × (x × y)] \mod n$
分配律	$[w × (x + y)] \mod n = [(w × x) + (w × y)] \mod n$
单位元	$(0 + w) \mod n = w \mod n$ $(1 × w) \mod n = w \mod n$
加法逆元	$\forall w \in Z_n$，存在 $z$ 使得 $w + z = 0 \mod n$

显然，要定义一个域，还需要一个乘法逆元的性质需要满足。

GF(p)

给定一个素数 $p$，元素个数为 $p$ 的有限域被定义为：整数 $\{0, 1, \ldots, p − 1\}$ 的集合 $Z_p$。其中，运算为模 $p$ 的算术运算。

乘法逆元

任意 $w \in Z_p$, 如果 $w \ne 0$，则存在 $z \in Z_p$，使得

$$ w \times z ≡ 1 \mod p $$

有了乘法逆元，$Z_p$ 就是一个有限域。接下来可以改造椭圆曲线了。

有限域上的椭圆曲线

椭圆曲线密码学是基于以下形式的方程：

$$ y^2 = (x^3 + a \times x + b) \mod p $$

可以看到这个式子只是对原式进行了简单的取模运算而已。下图是椭圆曲线 $y^2 = x^3 + 7$ 对素数 17 取模后的图像：

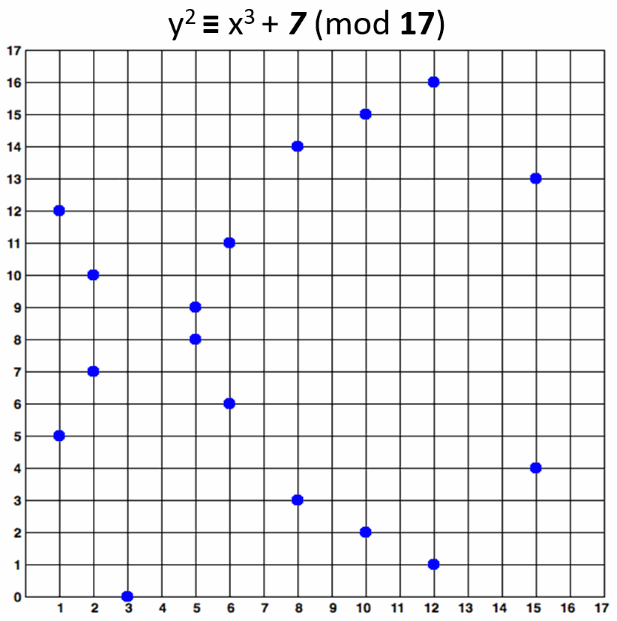
原本连续光滑的曲线变成了离散的点，但依然可以看到它也是关于某条水平直线对称的。

使用模运算改造前面实数域椭圆曲线的公式：

$$ s = \begin{cases} (3x_P^2+a)\times(2y_P)^{-1} \mod p & P = Q\\ (y_P - y_Q)\times(x_P - x_Q)^{-1} \mod p & P \ne Q \end{cases} $$

$$ x_R = (s^2 - x_P - x_Q) \mod p $$

$$ y_R = (y_P + s\times(x_R - x_P)) \mod p $$

def inv(a, b):
    """拓展欧几里得法求模逆元"""
    if b == 0:
        return a, 1, 0
    g, x, y = inv(b, a % b)
    if g != 1:
        raise ValueError
    x, y = y, x - a // b * y
    return g, x, y

def add(p1, p2):
    """椭圆曲线加法"""
    if p1 == p2:
        _, x, _ = inv(2 * p1[1], p)
        s = (((3 * p1[0] ** 2 + a) % p) * x) % p
    else:
        _, x, _ = inv(p1[0] - p2[0], p)
        s = (((p1[1] - p2[1]) % p) * x) % p
    rx = (s ** 2 - p1[0] - p2[0]) % p
    ry = (-p1[1] + s * (p1[0] - rx)) % p
    return rx, ry

示例

有下面一个椭圆曲线： $$ y^2=x^3+9x+17 \sim \mathbb{F}_{23} $$ 已知 $P=(16,5)$，$Q=(4,5)$，求 $k$，使得 $Q=kP$。

我们可以先验证一个 $P$，$Q$ 是否在这个曲线上：

$$ 5^2 \mod 23 = (16^3+9\times16+17) \mod 23 = 2 $$

$$ 5^2 \mod 23 = (4^3+9\times4+17) \mod 23 = 2 $$

已知 $a=9$，$p=23$，多次尝试计算不同的 $k$ 值：

a = 9
p = 23

for i in range(1, 10):
    r = double_and_add(i, (16, 5))
    print(f'{i}P = {r}')

脚本输出的计算结果：

1P = (16, 5)
2P = (20, 20)
3P = (14, 14)
4P = (19, 20)
5P = (13, 10)
6P = (7, 3)
7P = (8, 7)
8P = (12, 17)
9P = (4, 5)

经过我们的暴力计算，得出 $k = 9$。

离散对数

在上面的例子中，我们一个个尝试 $k$ 来求解等式。给定 $n$ 和 $P$，我们至少有一种多项式时间的算法可以计算 $Q = kP$。但是反过来呢？我们知道 $Q$ 和 $P$ 需要求解 $k$ 呢？这是一个离散对数问题。

给定素数 $p$ 和正整数 $g$，知道 $g^x \mod p$ 的值，求 $x$。

对于符合特定条件的 $p$ 和 $g$，这个问题是很难算的，更准确地说，是没有多项式时间的解法。

如果改一种记法，把椭圆曲线上点的加法记作乘法，原来的乘法就变成了幂运算，那么椭圆曲线上难题的形式跟离散对数问题应该是一致的。

尽管两个的形式一致，但是他们并不等价。实际上这个问题比大整数质因子分解（RSA）和离散对数（DH）难题都要难不少，目前还没有出现亚指数级时间复杂度的算法（大整数质因子分解和离散对数问题都有），这就是文章开头提到的同样甚至更高的安全强度下，椭圆曲线加密的密钥比 RSA 和 DH 的短不少的原因。

你知道 $P$ 和 $Q$，但是你无法据此求出 $k$，因为这里并没有椭圆曲线减法或者除法可用。你可以做成千上万次的加法，最终你只是知道在曲线上面结束的点，但是具体是如何到达这个点你也并不知道。你无法进行反向操作，得到相乘时的 $k$。

比如设 $k$ 为随机生成的大整数，作为私钥。选取一个已知的点 $G$，计算 $Q = k \times G$，用结果 $Q$ 作为公钥。公钥是可以公开的，即使别人知道公钥 $G$ 也无法推算出私钥 $k$。

这种即便你知道原点和终点，但是无法知道被乘数是 ECC 算法背后安全性的所有基础，而这一原则也被称为单向陷门函数。

参考

[1] 新手上路：实数上的椭圆曲线和群论

[2] 一文读懂 ECDSA 算法如何保护数据

[3] Elliptic curve

[4] How does one calculate the scalar multiplication on elliptic curves?

[5] Elliptic Curve Groups over Fp

[6] 离散对数和椭圆曲线加密原理

[7] ECC椭圆曲线加密算法：有限域和离散对数

[8] Field (mathematics)

[9] 现代密码学理论与实践